Movimento Bidimensional

Por Katson Wendell, Alexandre Montalvão e Priscila Souza

Continuando a discussão sobre cinemática das últimas semanas, hoje falamos sobre movimento em mais de uma dimensão, generalizando o tema da semana passada.

O movimento unidimensional que vimos anteriormente é um caso particular de uma classe mais ampla de movimentos que ocorrem em duas ou três dimensões. Se o movimento de um corpo está completamente restrito a um plano, ele é denominado movimento bidimensional. Neste caso, a posição é especificada através de coordenadas polares $(r, \theta)$ ou cartesianas $(x, y)$.

Para movimentos planos, as grandezas cinemáticas: posição $r$ (dado pelo ponto $(x,y)$), velocidade $v$ e aceleração $a$, não são necessariamente paralelas como acontece no movimento unidimensional. Desta forma, é de importância fundamental tratar estas grandezas vetorialmente. Assim, todas as grandezas até então definidas serão tratadas como vetores

$$\vec{v}_{méd}=\frac{\Delta \vec{r}}{\Delta t}$$

$$\vec{v}_{insta.}=\lim_{\Delta t\rightarrow0}\bigg(\frac{\Delta \vec{r}}{\Delta t}\bigg)_{t=t_{0}},$$ onde $\vec{r}=x\vec{i}+y\vec{j}$ é um vetor de posição relativo a um referencial qualquer.

$$\vec{a}_{méd}=\frac{\Delta \vec{v}}{\Delta t}$$

$$\vec{a}_{insta.}=\lim_{\Delta t\rightarrow0}\bigg(\frac{\Delta \vec{v}}{\Delta t}\bigg)_{t=t_{0}}.$$

A variação temporal de um vetor pode ser analisada através da variação temporal de suas componentes, da forma:  $$\vec{r}=x\vec{i}+y\vec{j}\Longrightarrow\vec{v}=\frac{dx}{dt}\vec{i}+\frac{dy}{dt}\vec{j}.$$ Lembre-se, os vetores unitários $\vec{i}$ e $\vec{j}$ não variam com o tempo.

Uma prática muito recorrente é a de decompor vetores, isto é útil, pois permite analisar o movimento independentemente. Por exemplo, $$\vec{v}=\frac{dx}{dt}\vec{i}+\frac{dy}{dt}\vec{j}=v_{x}\vec{i}+v_{y}\vec{j},$$ ou seja, a velocidade na direção $x$ só depende da variação da coordenada $x$ com o tempo, e a mesma coisa pode ser dita para a velocidade na direção $y$. Por isso, as equações do movimento retilíneo uniforme, ou uniformemente variado, podem ser utilizados no movimento bidimensional, pois tratamos tal movimento como sendo uma composição de outros dois movimentos. Por exemplo, no caso do lançamento de projéteis (desprezando a resistência do ar, ou tudo que atrapalhe o movimento), levando como referencial um plano cartesiano, temos uma composição de dois movimentos retilíneos, um acelerado através do eixo $y$ e outro uniforme na direção do eixo $x$. Por tanto, as equações destes dois movimentos são "renovados" com um caráter vetorial.

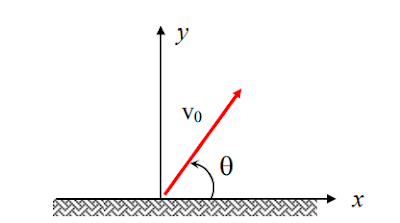
Um caso importante de movimento plano é aquele onde temos: $\vec{a}=-g\vec{j}$ (aceleração da gravidade)  que corresponde ao movimento de um corpo atirado de maneira arbitrária. Neste caso, o movimento será acelerado na direção $y$ e não acelerado nas demais. Vamos imaginar a situação em que o corpo é lançado obliquamente de maneira a formar um ângulo θ com a superfície, como mostrado na figura.

Lançamento de um projétil

Tomando-se o eixo $x$ paralelo à superfície e o eixo $y$ na vertical, a velocidade inicial $v_{0}$ pode ser decomposta em $v_{x}= v_{0} \cos{\theta}$ e $v_{y} = v_{0} \sin{\theta} $ . Na direção $x$ não existe aceleração, porém na direção $y$ temos $a_{y} = -g$ de modo que temos: 

$$\begin{cases}v_{x}(t)=v_{0}\cos{\theta}\\x(t)=x_{0}+v_{x}t=x_{0}+v_{0}\cos{\theta}t \end{cases}$$

e

$$\begin{cases}v_{y}(t)=v_{y}-gt=v_{0}\sin{\theta}-gt\\y(t)=y_{0}+v_{y}t-\frac{1}{2}gt^{2} \end{cases}$$

Eliminando-se o tempo do primeiro conjunto de equações $(t=\frac{x-x_{0}}{v_{x}} )$ e substituindo no segundo obtemos:  $$y=y_{0}+v_{y}\bigg(\frac{x-x_{0}}{v_{x}}\bigg)-\frac{1}{2}g\bigg(\frac{x-x_{0}}{v_{x}}\bigg)^{2}.$$ Que representa uma trajetória parabólica. A altura máxima pode ser calculada tomando-se $dy/dx = 0$. Portanto $$\frac{v_{y}}{v_{x}}-g\bigg(\frac{x-x_{0}}{v_{x}^{2}}\bigg)=0\Longrightarrow x=x_{max}=x_{0}+\bigg(\frac{v_{x}v_{y}}{g}\bigg)$$ e substituindo em $y(t)$ obtemos a expressão para a altura máxima atingida na trajetória: $$y=y_{max}=y_{0}+\frac{1}{2}\frac{v_{y}^{2}}{g}.$$

E é isso aí, pessoal. Na próxima semana falaremos sobre "Movimento Circular Uniforme". Nos vemos lá.

Referências

[1] Nussenzveig M.; Curso de Física Básica, vol. 1, 4ª Edição, pág. 324. Editora: EDGARD BLÜCHER LTDA. São Paulo, SP, 2002.

[2] Piórichkine A.V.; Ródina N.A. FÍSICA 1. U.R.S.S., 1984. 366 pág. Editora: Mir. Moscovo.