Equações do Movimento

Por Katson Wendell, Alexandre Montalvão e Priscila Souza

Continuando a discussão da semana passada sobre cinemática, hoje falaremos sobre as equações do movimento em si, ou seja, como descrever matematicamente o movimento. Nesta semana falaremos sobre movimento unidimensional e na próxima sobre movimento bidimensional.

Percebe-se que $x(t)$ não tem uma expressão definida, subentendendo que o caminho pode ser qualquer, porém vamos nos limitar a situações que envolvem velocidade e aceleração constante.

Movimento uniforme

Aquelas situações com velocidade constante e trajetória linear são denominadas de movimento retilíneo uniforme, de tal forma que utilizando a definição de velocidade obtemos a expressão horária da trajetória, ou seja, com $$v=\frac{\Delta x}{\Delta t}=\frac{x_{1}-x_{2}}{t_{1}-t_{2}},$$ onde $x_{i}=x(t_{i})$. 

Tomando $t_{1}$ como um instante $t$ qualquer e $t_{2}$ como um tempo inicial fixo $t_{0}$, implicando em uma posição inicial fixa $x(t_{0})=x_{0}$, obtemos uma expressão que dá a posição em qualquer instante de tempo $t$ 

$$x_{0}+v(t-t_{0})=x(t).$$

Lembrando que $v$ é constante (independente do tempo), ou seja, $v=\frac{dx}{dt}=c$, onde $c$ é uma constante. Gerando o gráfico de uma reta: 

$$c(t-t_{0})+x_{0}=x(t).$$

Movimento uniformemente acelerado

Agora trataremos de um movimento especial. Um movimento retilíneo chama-se uniformemente acelerado quando a aceleração instantânea é constante (independente do tempo): $a=\frac{dv}{dt}=\frac{d^{2}x}{dt^{2}}=c$. Nesta situação também há uma expressão horária que determina a trajetória e mais, a velocidade em função do tempo tem como gráfico uma reta. Para mostrar a dependência da velocidade no tempo, considere um movimento durante um intervalo de tempo $[t_{0},t]$, onde $t_{0}$ é o "instante inicial". Pela definição de aceleração instantânea, sabemos que $$v(t)-v(t_{0})=\int_{t_{0}}^{t} a dt=a(t-t_{0}),$$ lembre-se que $a$ é constante em relação ao tempo. Fazendo uma mudança de notação $v(t_{0})=v_{0},$ onde $v_{0}$ é um ponto fixo, temos 

$$v(t)=v_{0}+a(t-t_{0}).$$

Mostrando que a velocidade é uma função linear do tempo no movimento uniformemente acelerado.

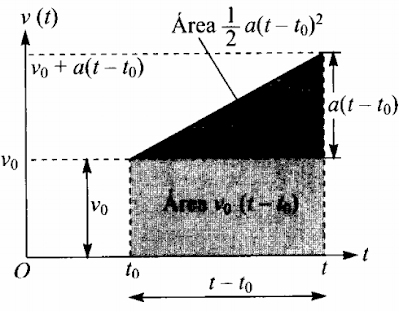
Encontramos uma das equações que engloba este tipo de movimento, mas falta expor a lei horária. Para expressar a lei horária devemos lembrar da definição de velocidade: $v(t)=\frac{dx(t)}{dt}.$ A partir desta definição podemos ver que, em uma trajetória $x(t)$ (onde sua velocidade está representada no figura 2.1) durante o intervalo de tempo $[t_{0},t]$, a variação da distância entre os extremos do intervalo é dado por

$$x(t)-x(t_{0})=\int_{t_{0}}^{t}v(t)dt.$$

Como o gráfico da velocidade em função do tempo é uma reta, fica fácil ver que a área associada a integral da velocidade, representada na figura 2.1, é um trapézio. De tal forma que podemos dividir este trapézio em outras duas formas geométricas: um triângulo e um retângulo. Portanto, a área do trapézio pode ser calculada como a soma da área do retângulo, isto é $v_{0}(t-t_{0})$, com a área do triângulo, que é $\frac{1}{2}(t-t_{0})a(t-t_{0})$, ou seja

$$\int_{t_{0}}^{t}v(t)dt=v_{0}(t-t_{0})+\frac{1}{2}(t-t_{0})a(t-t_{0})$$

$$\Longrightarrow x(t)-x(t_{0})=v_{0}(t-t_{0})+\frac{1}{2}(t-t_{0})a(t-t_{0}).$$ Definindo $x(t_{0})=x_{0}$, onde $x_{0}$ é um ponto fixo, temos a lei horária do movimento retilíneo uniformemente variado $$x(t)=x_{0}+v_{0}(t-t_{0})+\frac{1}{2}a(t-t_{0})^{2},$$ com condições iniciais sendo $x_{0}$ e $v_{0}$ em $t_{0}$. O gráfico $x\times t$ é uma parábola.

Integração da velocidade.

É interessante perceber que uma única substituição simples pode levar a uma expressão matematicamente vantajosa. A equação de Torricelli exprime a velocidade no movimento uniformemente acelerado como função da posição. Para obter esta expressão, basta substituir a equação

$$v(t)=v_{0}+a(t-t_{0})$$ em $$x(t)=x_{0}+v_{0}(t-t_{0})+\frac{1}{2}a(t-t_{0})^{2},$$ eliminando $t-t_{0}$: $$t-t_{0}=\frac{v-v_{0}}{a}$$

$$x(t)=x_{0}+v_{0}\bigg(\frac{v-v_{0}}{a}\bigg)+\frac{a}{2}\frac{(v-v_{0})^{2}}{a^{2}}$$

$$x - x_0 = \frac{v-v_{0}}{a}\bigg(v_{0}+\frac{v}{2}-\frac{v_{0}}{2}\bigg)=\frac{(v-v_{0})(v+v_{0})}{2a}=\frac{v^{2}-v_{0}^{2}}{2a}$$

$$\Longrightarrow v^{2}=v_{0}^{2}+2a(x-x_{0}).$$ Que é a expressão desejada.

E é isso aí, pessoal. Na próxima postagem falaremos sobre "Movimento Bidimensional". Nos vemos lá.

Referências

[1] Nussenzveig M.; Curso de Física Básica, vol. 1, 4ª Edição, pág. 324. Editora: EDGARD BLÜCHER LTDA. São Paulo, SP, 2002.